Bonus Certificates Tutorial
Introduction
Bonus certificates are designed to provide a predictable return in sideways markets, and market returns in rising markets.
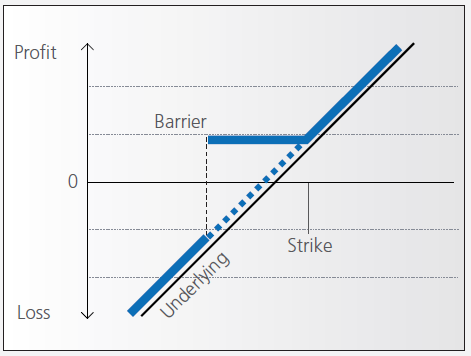
At the time they’re issued, bonus certificates normally have a term to maturity of two to four years. You will receive a specified cash pay-out (“bonus level” or “Strike”) if at maturity the price of the underlying is below or at the strike, as long as the underlying instrument has not touched or fallen below an established price level (“safety threshold” or “barrier”) during the term of the certificate.
Unless the certificate has a cap, you continue to participate in the price gains if the underlying instrument rises above the bonus level. In this case you either receive the corresponding number of shares or a cash settlement reflecting the value of the underlying instrument on the maturity date.
However, if the barrier is breached, you will no longer be entitled to the bonus payment. The value of the certificate then corresponds to the value of the underlying (times the ratio). In other words, once the barrier has been touched the certificate effectively converts to an index certificate. You will receive either the corresponding number of shares or a cash settlement reflecting the value of the underlying instrument on the maturity date.
Although there is no structured leverage, the presence of the barrier creates effective leverage. When the price of the underlying instrument approaches the barrier the probability of a breach increases, affecting the price of the certificate disproportionately.
Pay-out Profile
Example
Assume a bonus certificate on ABC share. The certificate has a strike of EUR 45.00 and a barrier set at EUR 36.00. The table below shows scenarios depending on the trading range of the underlying, the final price of the underlying and whether the barrier has been touched or not.
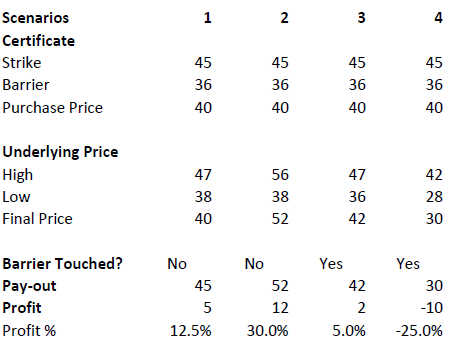
Warrant Tutorial
Introduction
A warrant confers the right to buy (call-warrant) or sell (put-warrant) a specific quantity of a specific underlying instrument at a specific price over a specific period of time.
Pay-out Profile
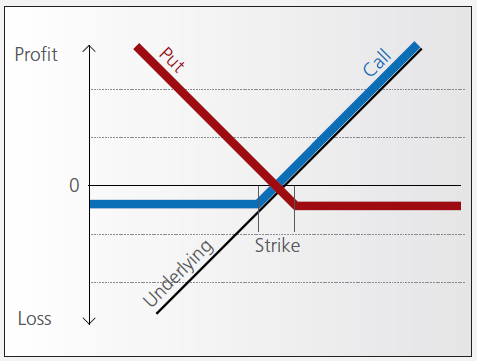
With some warrants, the option right can only be exercised on the expiration date. These are referred to as “European-style” warrants. With “American-style” warrants, the option right can be exercised at any time prior to expiration. The vast majority of listed warrants are cash-exercised, meaning that you cannot exercise the warrant to obtain the underlying physical share. The exception to this rule is Switzerland, where physically settled warrants are widely available.
IBKR does allow for US and Canadian warrant exercise. Customers wishing to do so should submit a Customer Service ticket stating the name/symbol of the warrant, the quantity of shares and the intended action (i.e. exercise). The broker will pass through all associated exercise costs to the customer upon completion of the request. US or Canadian warrants are not eligible for auto-exercise at expiration. Warrants remaining in an account at expiration will be removed as worthless.
Factors that influence pricing
Not only do changes in the price of the underlying instrument influence the value of a warrant, a number of other factors are also involved. Of particular importance to investors in this regard are changes in volatility, i.e. the degree to which the price of the underlying instrument fluctuates. In addition, changes in interest rates and the anticipated dividend payments on the underlying instrument also play a role.
However, changes in implied volatility - as well as interest rates and dividends - only affect the time value of a warrant. The primary driver - intrinsic value - is solely determined by the difference between the price of the underlying instrument and the specified exercise price.
Historical and implied volatility
In addressing this topic, a differentiation has to be made between historical and implied volatility. Implied volatility reflects the volatility market participants expect to see in the financial instrument in the days and months ahead. If implied volatility for the underlying instrument increases, so does the price of the warrant.
This is because the probability of profiting from a warrant during a particular time-frame increases if the price of the underlying instrument is highly volatile. The warrant is therefore more valuable.
Conversely, if implied volatility decreases, that leads to a decline in the value of warrants and hence occasionally to nasty surprises for warrant investors who aren’t familiar with the concept and influence of volatility.
Interest rates and dividends
Issuers hedge themselves against price changes in the warrant through purchases and sales of the underlying instrument. Due to the leverage afforded by warrants, the issuer needs considerably more capital to hedge its exposure than you require to buy the warrants. The issuer’s interest expense associated with that capital is included in the price of the warrant. The amount of embedded interest reduces over time and at expiration is zero.
In the case of puts, the situation is exactly the opposite. Here, the issuer sells the underlying instrument
short to establish the necessary hedge, and in so doing receives capital that can earn interest. Thus interest reduces the price of the warrant by an amount that decreases over time.
As the issuer owns shares as a part of its hedging operations, it is entitled to receive the related dividend
payments. That additional income reduces the price of call warrants and increases the price for puts. But if the dividend expectations change, that will have an influence on the price of the warrants. Unanticipated special dividends on the underlying instrument can lead to a price decline in the related warrants.
Key valuation factors
Let’s assume the following warrant:
Warrant Type: Call
Term to expiration: 2 years
Underlying : ABC Share
Share price: EUR 30.00
Strike: EUR 30.00
Exercise ratio: 0.1
Warrant’s price: EUR 0.30
Intrinsic value
Intrinsic value represents the amount you could receive if you exercised the warrant immediately and then bought (in the case of a call) or sold (put) the underlying instrument in the open market.
It’s very easy to calculate the intrinsic value of a warrant. In our example the intrinsic value is EUR 00.00
and is calculated as follows:
(price of underlying instrument – strike price) x exercise ratio
= (EUR 30.00 – EUR 30.00) x 0.1
= EUR 00.00
If the price of the ABC share increases by EUR 1, the intrinsic value becomes
= (EUR 31.00 – EUR 30.00) x 0.1
= EUR 00.10
The intrinsic value of a put warrant is calculated with this formula:
(strike price – price of underlying instrument) x exercise ratio
It’s important to note that the intrinsic value of a warrant can never be negative. By way of explanation:
if the price of the underlying instrument is at or below the exercise price, the intrinsic value of a call equals zero. In this instance, the price of the warrant consists only of “time value”. On the flipside, the intrinsic value of a put is equal to zero if the price of the underlying instrument is at or above the exercise price.
Time value
Once you’ve calculated the intrinsic value of a warrant, it’s also easy to figure out what the time value of that warrant is. You simply deduct the intrinsic value from the current market price of the warrant. In our example, the time value is equal to EUR 1.30 as you can see from the following calculation:
(warrant price – intrinsic value)
= (EUR 0.30 EUR – EUR 0.00)
= EUR 0.30
Time value gradually erodes during the term of a warrant and ultimately ends up at zero upon expiration. At that point, warrants with no intrinsic value expire worthless. Otherwise you can expect to receive payment of the intrinsic value. Take note, though: a warrant’s loss of time value accelerates during the final months of its term.
Premium
The premium indicates how much more expensive a purchase/sale of the underlying instrument would be via the purchase of a warrant and the immediate exercise of the option right as opposed to simply buying/selling the underlying instrument in the open market.
Hence the premium is a measure of how expensive a warrant actually is. It follows that, when given a choice between warrants with similar features, you should always buy the one with the lowest premium. By calculating the premium as an annualized percentage, warrants with different terms to expiry can be compared with each other.
The percentage premium for the call warrant in our example can be calculated as follows:
(strike price + warrant price / exercise ratio – share price) / share price * 100
= (EUR 30.00 + EUR 0.30 / 0.1 – EUR 30.00) / EUR 30.00 x 100
= 10 percent
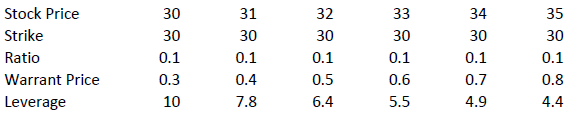
Leverage
The amount of leverage is the price of the share * ratio divided by the price of the warrant. In our example 30.00*0.1/0.3 = 10. So when the price of ABC increases by 1% the value of the warrant increases by 10%.
The amount of leverage is not constant however; it varies as intrinsic and time value changes, and is particularly sensitive to changes in intrinsic value. As a rule of thumb, the higher the intrinsic value of the warrant, the lower the leverage. For example (assuming constant time value):
Knock-out (Turbo) Tutorial
Introduction
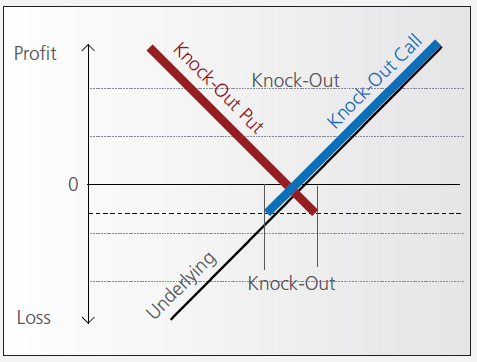
Knock-out warrants (turbos), like vanilla warrants, derive their value from the difference between the price of the underlying and the strike. They differ significantly however from vanilla warrants in many important respects:
- They can expire (knock-out) prematurely if the price of the underlying instrument touches or falls below (in the case of knock-out calls) or exceeds (in the case of knockout puts) a predetermined barrier-level. It expires worthless if the barrier equals the strike, or it may have a residual stop-loss value if the barrier is set higher than the strike (in the case of a call).
- Changes in implied volatility have little or no impact on knock-out products, therefore their pricing is easier for investors to comprehend than that of warrants.
- They have little or no time value (because of the presence of the knock-out barrier), and therefore have a higher degree of leverage than a warrant with the same strike. This is because the absence of time value makes the instrument “cheaper”.
Pay-out Profile
Leverage
As discussed above, knock-out warrants exhibit high degrees of leverage, particularly as the price of the underlying nears the strike/barrier. Consider the following example of a long turbo on the Dow Jones Index, compared to a vanilla warrant:
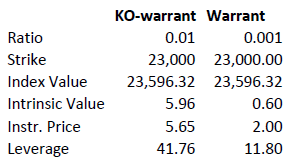
Intrinsic value = (index value – strike) x ratio
Leverage = Index Value x Ratio / Instrument Price
A vanilla warrant retains significant time value even as the underlying price approaches the strike, sharply reducing its leverage compared to a knock-out warrant.
Product types
As discussed above, the barrier may either equal the strike, or be set above (calls) or below (puts). In the latter cases a small residual value remains after knock-out, corresponding to the difference between the barrier (the stop-loss level) and the strike.
Moreover, knock-out products may either have an expiration date or may be open-ended. This makes a difference in the way interest is accounted for. If the contract has an expiration date interest is included in the premium, the amount of which reduces over time and is zero on expiration. This is analogous to a standard vanilla warrant.
in relation to an expiration date. The price of the contract therefore corresponds exactly to its intrinsic value. Interest however must be accounted for. This is done by a daily adjustment of the barrier and strike. The following example shows the daily adjustment for a long open-end turbo on the Dow Jones Index:
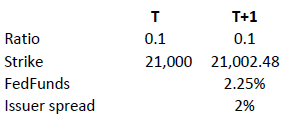
The adjustment = Strike T x (1+ FedFunds/360 + Issuer Spread/360).
The intrinsic value of the instrument is correspondingly reduced as follows, assuming no change in the value of the DJ Index):
Intrinsic value = (index value – strike) x ratio
Discount Certificates Tutorial
Introduction
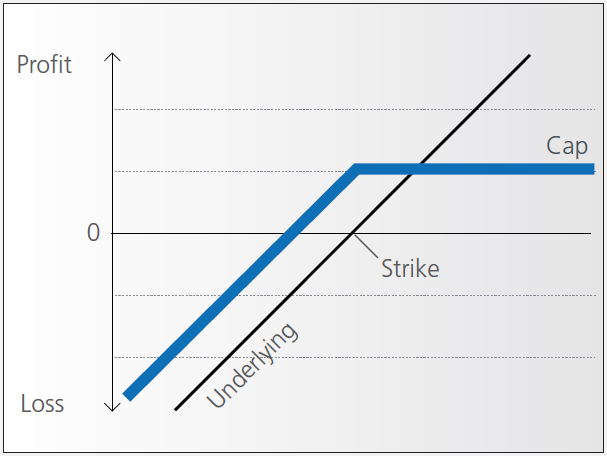
Discount certificates are designed to provide an enhanced return in sideways markets, compared to a direct investment in the underlying.
Discount certificates make it possible for you to buy an underlying instrument for less than its current market price. However, the maximum payback on a discount certificate is limited to a predetermined amount (cap).
Discount certificates normally have a term to maturity of one to three years. At maturity, a determination is made of where the price of the underlying instrument stands.
If it is at or above the cap, you’ll earn the maximum return and receive payment of the amount reflected by the cap.
If the price of the underlying instrument is below the cap on the maturity date, you’ll receive either the corresponding number of shares or a cash settlement reflecting the value of the underlying instrument on the maturity date.
Pay-out Profile
Example
Assume a discount certificate on ABC share. The certificate has a cap of EUR 40.00, and a purchase price of EUR 36.00. The table below shows scenarios depending on the final price of the underlying.
Factor Certificates Tutorial
Introduction
Factor certificates employ a daily leverage factor that multiplies the daily performance of the underlying instrument. Unlike knock-out warrants and mini-futures, factor certificates do not have a knock-out barrier. To avoid a loss greater than the investment, the calculation resets intraday if the performance of the underlying threatens to render the certificate worthless.
Daily Leverage
The performance of the certificate is calculated daily, without reference to previous days’ values. If the underlying returns 1% on the day, the value of 3x certificate increases by 3%, a 5x by 5%. The next day the process is repeated, referencing the prior day’s underlying close.
As such, factor certificates are particularly suitable for day-traders.
However, for a period of more than one day, the cumulative performance of the underlying cannot be simply multiplied by a factor of 3 as the previous day’s price always forms the new basis of calculating each day’s performance for the certificate. To illustrate with an example:
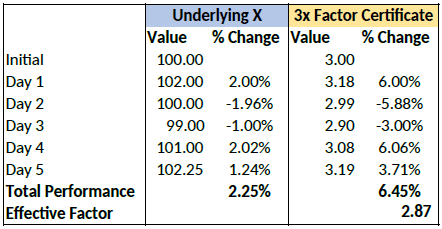
Cumulatively, the factor certificate has returned less than 3x the performance of the underlying.
Intraday Reset
If an underlying for a factor certificate loses more than a certain percentage of its value intraday, the calculation is reset by simulating a new day. The reset threshold varies depending on the leverage factor.
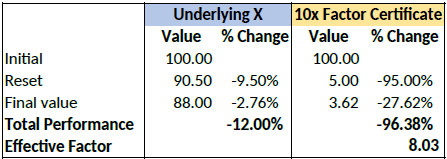
Let’s assume a long factor certificate with a 10x leverage factor. According to the terms of the certificate, a reset will be triggered if the underlying loses more than 9.5% during the calculation day.
Let’s now assume that the underlying loses 12% of its value during a particular day. The reset
and final performance will be as follows:
Complex Position Size
For complex, multi-leg options positions comprising two or more legs, TWS might not track all changes to this position, e.g. a vertical spread where the short leg is assigned and the user re-writes the same leg the next day, or if the user creates a the position over multiple trades, or if the order is not filled as a native combination at the exchange.
If you received a message because you are submitting an order to close a position, roll a position, or modify a position using the “% Change” feature, it means that the maximum quantity of option positions in your account that are available to close for this order is different from that of the original position tracked by TWS.
Before submitting, you should review the order and confirm that the order quantity we have calculated is the correct quantity that you want to trade.
為何美國期權的佣金收費各有不同？
IB的期權佣金費用包含兩部分：
1. 歸於IB的執行費用。 對於智能傳遞定單，該費用為每份合約$0.70美元，給定月份超出100,000份合約的定單，每份合約可低至$0.15美元（參見網站了解直接傳遞定單費用、低價期權優惠費率和最低定單費用）；
2. 第三方交易所、監管和/或交易費用。
就第三方費用而言，某些美國的期權交易所會有一個流動性費用/折扣結構，在與IB的執行費用以及其他監管和/或交易費用一起應用時，可能會導致各個定單總的每份合約佣金費用各不相同。 這是由交易所部分的計算所造成的。交易所部分的計算最終結果可能是向客戶支付款項而非收取費用，其取決於一些不受IB控制的因素，包括客戶的定單屬性以及現行買-賣報價。
採用這種流動性費用/折扣模式的交易所會對消耗流動性的定單（即適銷定單）收取費用，而對添加流動性的定單（即非適銷的限價定單）提供折扣返點。費用會因交易所、客戶類型（如公眾客戶、經紀交易商、公司、做市商和專業交易者）和期權底層證券的不同而不同，公眾客戶折扣通常介於$0.10 - $0.42之間，而公眾客戶費用則介於$0.15 - $0.50之間。
IB有義務將適銷的期權定單傳遞至提供最佳執行價格的交易所，且如果出現多個最佳報價，智能傳遞在決定將定單傳往哪個交易所時會考慮流動性消耗費用（即會將定單傳遞至費用最低或無費用的交易所）。 因此，只有在提供的價格優於市價至少$0.01時，智能傳遞才會將市價定單傳遞至收取更高費用的交易所（鑑於標準期權乘數為100，會產生$1.00的價格改善，大於最高流動性消耗費用）。
有關添加/消耗流動性概念的更多信息以及相關舉例，請參見KB201。
添加/消耗流動性
Overview:
本文旨在對交易所費用、添加/消耗流動性費用以及非組合佣金提供正確的理解。
添加或消耗流動性的概念既適用於股票，也適用於股票/指數期權。一個定單是消耗流動性還是添加流動性，取決於定單是適銷還是非適銷。
適銷定單會消耗流動性。
適銷定單要么是市價定單，要么是限價等於或高於/低於當前市價的買入/賣出限價定單。
1. 對於適銷的買入限價定單，限價等於或高於賣價。
2. 對於適銷的賣出限價定單，限價等於或低於買價。
舉例：
XYZ股票當前賣價尺寸/價格為400股/46.00。您輸入一個買入限價定單，即以46.01的價格買入100股XYZ股票。由於定單馬上就能執行，其將被視為適銷定單。如果交易所會對消耗流動性收費，則客戶將需繳納該費用。
非適銷定單會添加流動性。
非適銷定單是限價低於/高於當前市價的買入/賣出限價定單。
1. 對於非適銷的買入限價定單，限價低於賣價。
2. 對於非適銷的賣出限價定單，限價高於買價。
舉例：
XYZ股票當前賣價尺寸/價格為400股/46.00。您輸入一個買入限價定單，即以45.99的價格買入100股XYZ股票。由於定單將被作為最佳買價發布至市場，而不會立即執行，其將被視為非適銷定單。
若有人發送了一個適銷的賣出定單，從而使您的買入限價定單得以執行，則如果有添加流動性返點，您會收到一定折扣（返點）。
請注意：
1. 所有交易期權的賬戶均需就消耗/添加流動性繳納/享受期權交易所費用或返點。
2. 根據IB網站，消耗/添加流動性費用表下只有負數才是折扣（返點）。
https://www.interactivebrokers.com.hk/cn/index.php?f=2356
非適銷定單是限價低於/高於當前市價的買入/賣出限價定單。
1. 對於非適銷的買入限價定單，限價低於賣價。
2. 對於非適銷的賣出限價定單，限價高於買價。
舉例：
XYZ股票當前賣價尺寸/價格為400股/46.00。您輸入一個買入限價定單，即以45.99的價格買入100股XYZ股票。由於定單將被作為最佳買價發布至市場，而不會立即執行，其將被視為非適銷定單。
若有人發送了一個適銷的賣出定單，從而使您的買入限價定單得以執行，則如果有添加流動性返點，您會收到一定折扣（返點）。
請注意：
1. 所有交易期權的賬戶均需就消耗/添加流動性繳納/享受期權交易所費用或返點。
2. 根據IB網站，消耗/添加流動性費用表下只有負數才是折扣（返點）。
https://www.interactivebrokers.com.hk/cn/index.php?f=2356
股票與期權佣金/費用請參見上方鏈接。
Risks of Volatility Products
Trading and investing in volatility-related Exchange-Traded Products (ETPs) is not appropriate for all investors and presents different risks than other types of products. Among other things, ETPs are subject to the risks you may face if investing in the components of the ETP, including the risks relating to investing in complex securities (such as futures and swaps) and risks associated with the effects of leveraged investing in geared funds. Investors should be familiar with the diverse characteristics of each ETF, ETN, future, option, swap and any other relevant security type. We have summarized several risk factors (as identified in prospectuses for ETPs and in other sources) and included links so you can conduct further research. Please keep in mind that this is not a complete list of the risks associated with these products and investors are responsible for understanding and familiarizing themselves completely before entering into risk-taking activities. By providing this information, Interactive Brokers (IB) is not offering investment or trading advice regarding ETPs to any customer. Customers (and/or their independent financial advisors) must decide for themselves whether ETPs are an appropriate investment for their portfolios.
An ETP may not be benchmarked to the index it appears to track
"An investor should only consider an investment in a Fund if he or she understands the consequences of seeking exposure to VIX futures contracts. The Funds are benchmarked to the S&P VIX Short-Term Futures Index, an investable index of VIX futures contracts. The Funds are not benchmarked to the VIX Index. The VIX Index is a non-investable index that measures the implied volatility of the S&P 500. For these purposes, "implied volatility" is a measure of the expected volatility (i.e., the rate and magnitude of variations in performance) of the S&P 500 over the next 30 days. The VIX Index does not represent the actual volatility of the S&P 500. The VIX Index is calculated based on the prices of a constantly changing portfolio of S&P 500 put and call options. The Index underlying each Fund consists of short-term VIX futures contracts. As such, the performance of the Index and the Funds can be expected to be very different from the actual volatility of the S&P 500 or the performance of the VIX Index." [Page 1]
"… your ability to benefit from any rise or fall in the level of the VIX Index is limited. The Index underlying your ETNs is based upon holding a rolling long position in futures on the VIX Index. These futures will not necessarily track the performance of the VIX Index. Your ETNs may not benefit from increases in the level of the VIX Index because such increases will not necessarily cause the level of VIX Index futures to rise. Accordingly, a hypothetical investment that was linked directly to the VIX Index could generate a higher return than your ETNs." [Page PS-12]
ETPs may not provide a suitable hedge
"Historical correlation trends between the Index and other asset classes may not continue or may reverse, limiting or eliminating any potential diversification or other benefit from owning a Fund." [Page 20]
Volatility based ETPs are volatile in themselves and are not intended for long term investment
"… investments can be highly volatile and the Funds may experience large losses from buying, selling or holding such investments. ... In addition, gains, if any, may be subject to significant and unexpected reversals. The Funds generally are intended to be used only for short-term investment horizons. As with all investments, an investor in any of the Funds could potentially lose the full principal value of his/her investment, even over periods as short as one day." [Page 1]
"The ETNs are only suitable for a very short investment horizon. The relationship between the level of the VIX Index and the underlying futures on the VIX Index will begin to break down as the length of an investor’s holding period increases, even within the course of a single Index Business Day. ... The ETNs are not long term substitutes for long or short positions in the futures underlying the VIX Index. ... The long term expected value of your ETNs is zero. If you hold your ETNs as a long term investment, it is likely that you will lose all or a substantial portion of your investment. " [Page PS-15]
The use of leveraged positions could result in the total loss of an investment
"The Ultra Fund utilizes leverage in seeking to achieve its investment objective and will lose more money in market environments adverse to its respective daily investment objectives than funds that do not employ leverage…
For example, because the Ultra Fund includes a two times (2x) multiplier, a single-day movement in the Index approaching 50% at any point in the day could result in the total loss or almost total loss of an investor’s investment if that movement is contrary to the investment objective of the Fund, even if the Index subsequently moves in an opposite direction, eliminating all or a portion of the movement…
Inverse positions can also result in the total loss of an investor’s investment. For the Inverse Fund, a single-day or intraday increase in the level of the Fund’s benchmark approaching 100% could result in the total loss or almost total loss of an investor’s investment, even if such Fund’s benchmark subsequently moves lower. " [Page 14]
Possible illiquid markets may exacerbate losses
"Financial Instruments cannot always be liquidated at the desired price. It is difficult to execute a trade at a specific price when there is a relatively small volume of buy and sell orders in a market. A market disruption can also make it difficult to liquidate a position or find a swap counterparty at a reasonable cost. " [Page 17]
Short covering may intensify losses in volatility-related ETPs
In the event of a sudden market volatility change, many traders with positions in volatility-related products will incur substantial unexpected losses. These losses may cause them to choose to close their positions. The losses may also result in margin deficits and subsequent liquidations of some or all positions. Such closing trades will add to the movement of these products. Since speculative interest in the VIX is at an all-time high, there may be no precedent for what will happen if volatility moves quickly.
The Commodity Futures Trading Commission's (CFTC) weekly Commitments of Traders (COT) report provides a breakdown of the net positions for "non-commercial" (speculative) traders in U.S. futures markets. As of September 2017 CFTC reported VIX speculative net short is at an all-time high.
"Despite the fact that the average daily closing value of the CBOE Volatility Index (VIX) is about 11.5 so far this year, VIX futures and options both had record days for volume and for open interest this month. … VIX futures hit a new record for open interest with more than 673,000 contracts on August 7 (2017), and VIX options reached a new record for open interest with 14,783,380 contracts open on August 15 (2017)."
*As this data is constantly changing, investors in volatility-related products should regularly check for updates.
ETP issuers may redeem shares for cash in the event of extreme moves
"The Intraday Indicative Value on any Index Business Day could be reduced to 20% or less of the prior day’s Closing Indicative Value. If this occurs, we may choose to exercise our right to effect an Event Acceleration of the ETNs for an amount equal to that day’s Closing Indicative Value and you may not receive any of your initial investment." [Page PS-17]
